التسلسلات والأنماطأرقام فيبوناتشي
تخيل أنك تلقيت زوجًا من الأرانب الصغيرة ، ذكرا وأنثى. هم أرانب خاصة جدًا ، لأنهم لا يموتون أبدًا ، والأنثى تلد زوجًا جديدًا من الأرانب مرة واحدة كل شهر بالضبط (دائمًا زوج آخر من الذكور والإناث).




















في الشهر التالي ، سيكون لديك 13 زوجًا من الأرانب: 8 أزواج من الشهر السابق ، بالإضافة إلى 5 مجموعات جديدة من الأطفال. هل يمكنك اكتشاف نمط في هذا التسلسل؟
عدد الأرانب في شهر معين هو
هل يمكنك حساب عدد الأرانب بعد بضعة أشهر أخرى؟
1, 1, 2, 3, 5, 8,
بعد 12 شهرًا ، سيكون لديك 144 زوجًا من الأرانب!
يُطلق على تسلسل الأرقام هذا
عندما ولد فيبوناتشي عام 1175 ، كان معظم الناس في أوروبا لا يزالون يستخدمون
عندما عاد إلى إيطاليا ، كتب فيبوناتشي كتابًا بعنوان Liber Abaci (اللاتينية "كتاب الحسابات") ، حيث قدم لأول مرة الأرقام العربية الجديدة للتجار الأوروبيين. لقد حققوا نجاحًا فوريًا - وما زلنا نستخدمهم اليوم.
في إحدى صفحات كتابه ، حقق أيضًا في أنماط تكاثر الأرانب - ولهذا السبب تم تسمية أرقام فيبوناتشي باسمه.
صفحات من فيبوناتشي Liber Abaci
بالطبع ، أرقام فيبوناتشي ليست هي الطريقة التي يملأ بها الأرانب في الواقع في الحياة الحقيقية. لا تمتلك الأرانب ذكورًا واحدًا ونسلًا واحدًا كل شهر ، ولم نحسب سبب وفاة الأرانب في نهاية المطاف.
ولكن اتضح أن هناك العديد من الأماكن الأخرى في الطبيعة حيث تظهر أرقام فيبوناتشي: على سبيل المثال اللوالب في النباتات. هل يمكنك حساب عدد اللوالب الموجودة في كل اتجاه؟
يحتوي مخروط الصنوبر هذا على
يحتوي عباد الشمس هذا على 34 لولبًا باتجاه عقارب الساعة و 55 لولبًا بعكس اتجاه عقارب الساعة.
في كلتا الحالتين ، أعداد اللوالب هي أرقام فيبوناتشي متتالية. وينطبق الشيء نفسه على العديد من النباتات الأخرى: في المرة القادمة التي تخرج فيها ، احسب عدد البتلات في الزهرة أو عدد الأوراق على الساق. في كثير من الأحيان ستجد أنها أرقام فيبوناتشي!
بالطبع ، هذه ليست مجرد مصادفة. هناك سبب مهم لماذا تحب الطبيعة تسلسل فيبوناتشي ، والذي ستتعلم المزيد عنه لاحقًا.
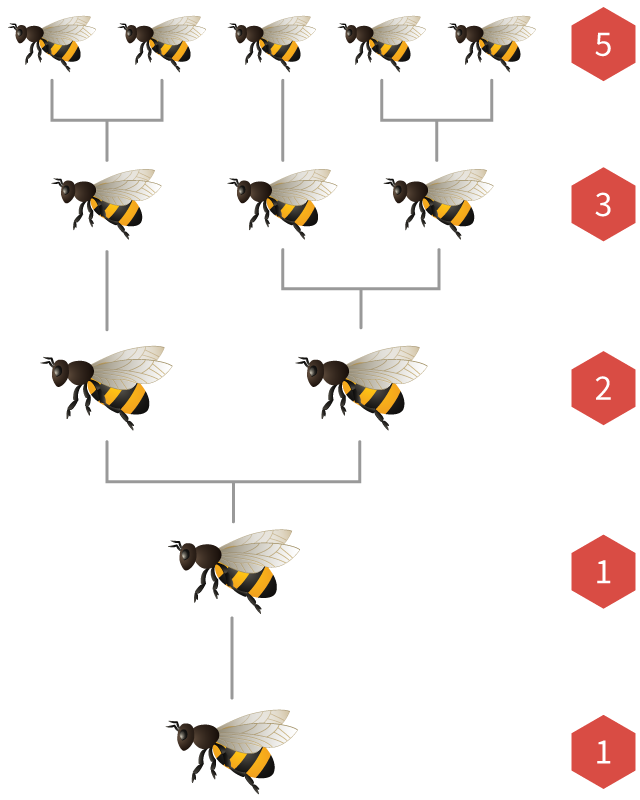
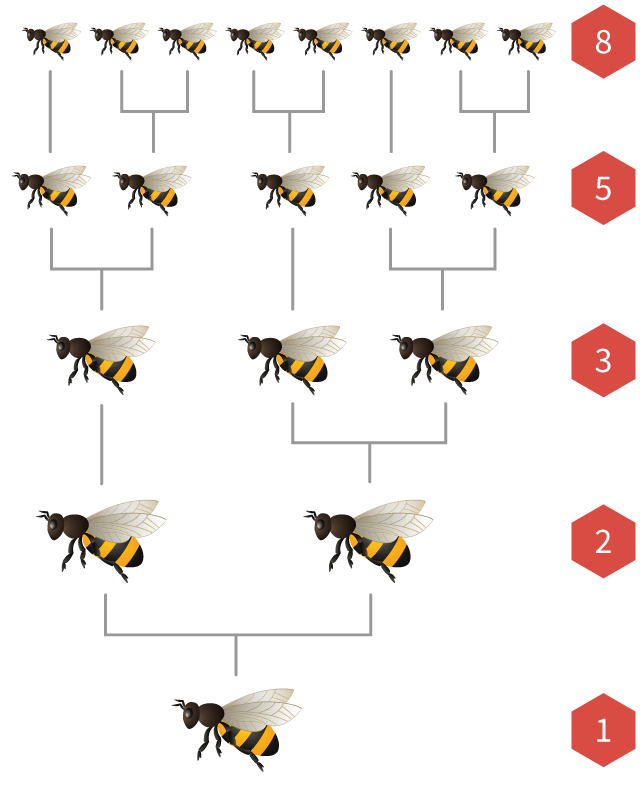
تظهر أرقام فيبوناتشي أيضًا في مجموعات نحل العسل.
يوجد في كل مستعمرة نحل ملكة واحدة تضع الكثير من البيض. إذا تم تخصيب بيضة بواسطة نحلة ذكر ، فإنها تفقس في نحلة أنثى. إذا لم يتم تخصيبها ، فإنها تفقس في نحلة ذكر (تسمى طائرة بدون طيار).
وهذا يعني أن النحل لدى الإناث
إذا رسمنا شجرة النحل ، فإن عدد الآباء والأجداد والأجداد والأجيال السابقة دائمًا ما يكون أرقام فيبوناتشي!
في بعض الأحيان ، تتغذى النحل الشابة على طعام خاص يسمى "غذاء ملكات النحل". في هذه الحالة ، يتحولون إلى ملكات وسيطيرون بعيدًا لبدء خلية جديدة.
النسبة الذهبية
تمامًا مثل
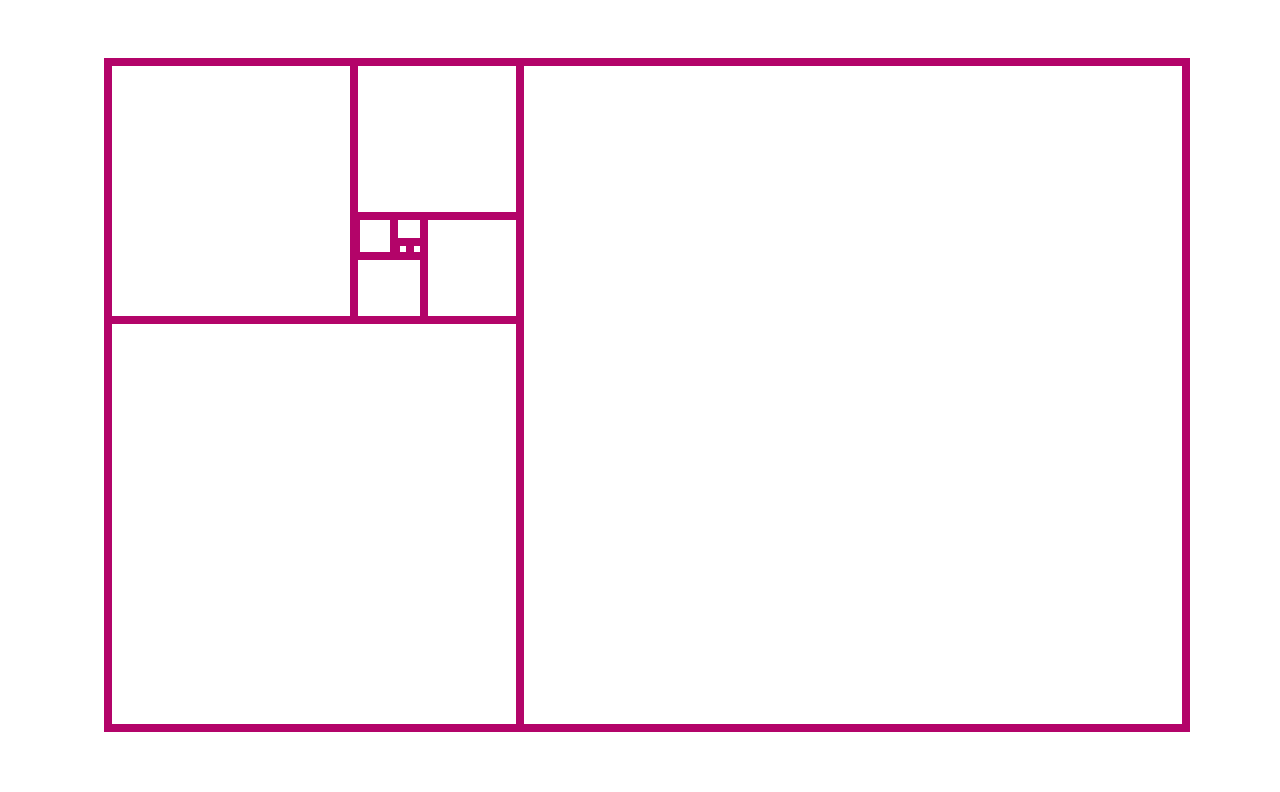
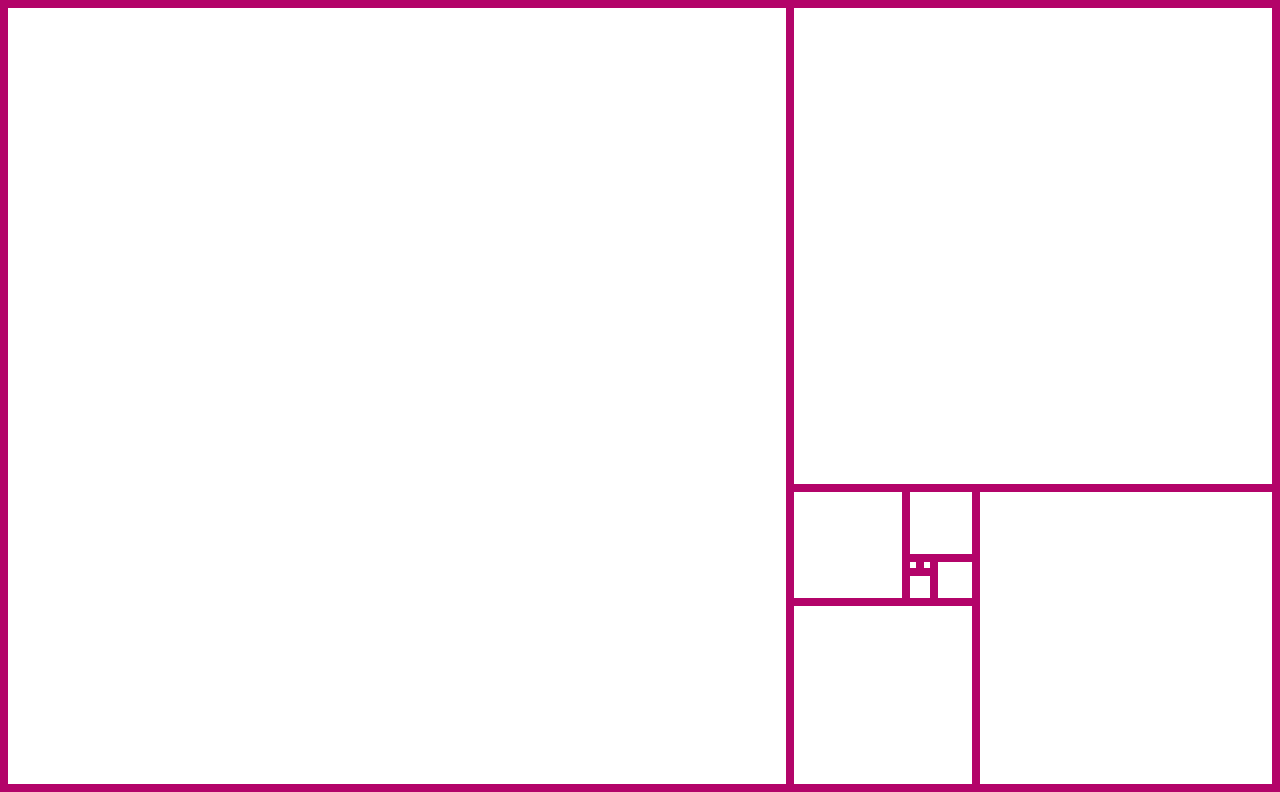
في كل خطوة ، تشكل المربعات مستطيلًا أكبر. عرضه وارتفاعه دائمًا رقمان فيبوناتشي متتاليان. نسبة العرض إلى الارتفاع للمستطيل هي نسبة عرضه وارتفاعه:
لاحظ كيف ، عندما نضيف المزيد والمزيد من المربعات ، يبدو أن نسبة العرض إلى الارتفاع تقترب من رقم معين حول 1.6. يُسمى هذا الرقم
يعتقد الكثير من الناس أن النسبة الذهبية ممتعة بشكل خاص من الناحية الجمالية. لهذا السبب يتم استخدامه غالبًا من قبل الفنانين والمهندسين المعماريين - كما هو الحال في هذين المثالين:
قيل أن النحات اليوناني فيدياس استخدم النسبة الذهبية عند تصميم بارثينون في أثينا. الحرف الأول من اسمه
سر العشاء الأخير للفنان الإسباني سلفادور دالي ، هو واحد من العديد من اللوحات ذات النسبة الذهبية. في الخلفية ، يمكنك أيضًا مشاهدة
يمكننا تقريب النسبة الذهبية من خلال
ومع ذلك ، اتضح أنه لا يمكن كتابة القيمة الدقيقة لـ
لوالب فيبوناتشي
توضح النسبة الذهبية سبب ظهور أرقام فيبوناتشي في الطبيعة ، مثل عباد الشمس ومخروط الصنوبر الذي رأيته في بداية هذا القسم.
ينمو هذان النباتان للخارج من مركزهما (جزء من النبات يسمى meristem). عند إضافة بذور أو أوراق أو بتلات جديدة ، فإنها تدفع البذور الموجودة إلى الخارج.
حرك المنزلق على اليمين لتصور كيف ينمو النبات. لاحظ كيف تتم إضافة كل ورقة في دوران مختلف عن الدوران السابق. دائمًا ما تكون الزاوية بين ورقتين متتاليتين هي نفسها.
من المهم للزهور اختيار زاوية مناسبة: يجب أن تكون الأوراق أو البذور متباعدة بشكل متساوٍ تقريبًا حتى تحصل على أكبر قدر من ضوء الشمس والمغذيات. في الرسم البياني أدناه ، يمكنك استكشاف الشكل الذي قد تبدو عليه عباد الشمس بزوايا مختلفة بين بذورها:
قد تتذكر من الأعلى أن نسب أرقام فيبوناتشي المتتالية تقترب أكثر وأكثر من النسبة الذهبية - ولهذا السبب ، إذا كنت تحسب عدد اللوالب في النبات ، فغالبًا ما ستجد رقم فيبوناتشي.
من المهم أن نتذكر أن الطبيعة لا تعرف عن أرقام فيبوناتشي. لا تستطيع الطبيعة أيضًا حل المعادلات لحساب النسبة الذهبية - ولكن على مدار ملايين السنين ، كان للنبات الكثير من الوقت لتجربة زوايا مختلفة واكتشاف أفضلها.
تريد النباتات والحيوانات دائمًا النمو بأكثر الطرق كفاءة ، ولهذا السبب تمتلئ الطبيعة بالأنماط الرياضية المنتظمة.
فيبوناتشوس
حتى الآن ، استخدمنا فقط المعادلة العودية لأرقام فيبوناتشي. في الواقع هناك معادلة صريحة أيضًا - ولكن من الصعب العثور على:
يمكننا أيضًا محاولة اختيار نقاط بداية مختلفة لأرقام فيبوناتشي. على سبيل المثال ، إذا بدأنا بـ 2 ، 1 ، ... بدلاً من 1 ، 1 ، ... نحصل على تسلسل يسمى أرقام لوكاس.
اتضح أنه ، بغض النظر عن رقمي البدء اللذين تختارهما ، فإن التسلسلات الناتجة تشترك في العديد من الخصائص. على سبيل المثال ، تتقارب نسب المصطلحات المتتالية دائمًا
هناك العديد من الألغاز والأنماط والتطبيقات الأخرى المتعلقة بأرقام فيبوناتشي. إليك بعض الأمثلة التي يمكنك تجربتها بنفسك:
Problem solving
1. انقسام فيبوناتشي
(أ) ما هي أرقام فيبوناتشي حتى؟ هل هناك نمط حيث يتم وضعهم على طول التسلسل؟ هل يمكنك أن تشرح لماذا؟
(ب) أي أرقام فيبوناتشي قابلة للقسمة على 3 (أو قابلة للقسمة على 4)؟ ماذا تلاحظ؟
2. مبالغ فيبوناتشي
ماذا يحدث إذا جمعت أي ثلاثة أرقام متتالية في فيبوناتشي؟ هل يمكنك أن تشرح لماذا؟
3. سلالم فيبوناتشي
عند صعود الدرج ، يمكنني إما أن أخطو خطوة واحدة أو أقفز بخطوتين في كل مرة. هذا يعني أن هناك العديد من الاحتمالات المختلفة لكيفية صعود الدرج. على سبيل المثال ، إذا كانت هناك 5 خطوات ، فلدي 8 خيارات مختلفة:
كم عدد الخيارات للدرج مع 6 أو 7 أو 8 خطوات؟ هل يمكنك اكتشاف نمط؟ وكيف يرتبط هذا بأرقام فيبوناتشي؟
© FoxTrot, by Bill Amend