التسلسلات والأنماطتسلسلات حسابسة و هندسية

في عام 1682 ، لاحظ الفلكي إدموند هالي ظاهرة غير عادية: جسم أبيض متوهج وذيل طويل يتحرك عبر سماء الليل. كان مذنبًا ، صخرة جليدية صغيرة تحلق عبر الفضاء ، بينما تترك وراءها دربًا من الغبار والجليد.

تذكر هالي أن علماء الفلك الآخرين لاحظوا مذنبات مشابهة في وقت أبكر بكثير: واحدة عام 1530 وأخرى عام 1606. لاحظ أن الفجوة بين ملاحظتين متتاليتين هي نفسها في كلتا الحالتين: سنة.

صورة مذنب هالي
اتخذت في عام 1986 قي جزيرة الفصح

وخلص هالي إلى أن جميع الملاحظات الثلاث كانت في الواقع من نفس المذنب - الذي يُطلق عليه الآن مذنب هالي. تدور حول الشمس وتمرر الأرض كل 76 عامًا تقريبًا. كما توقع متى سيكون المذنب مرئيًا بعد ذلك:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

في الواقع ، الفاصل الزمني ليس دائمًا بالضبط 76 عامًا: يمكن أن يختلف باختلاف سنة أو سنتين ، حيث تتقاطع مدار المذنب مع الكواكب الأخرى. نعلم اليوم أن مذنب هالي لاحظه علماء الفلك القدماء في وقت مبكر من 240 قبل الميلاد!

قطع مذنب ّالي على مر الزمن: لوح بابلي (164 قبل الميلاد نسيج ((1070, مجلة علمية (1910, وختم سوفيتي (1986) ).

تبحث مجموعة مختلفة من العلماء في سلوك كرة التنس المرتدة. أسقطوا الكرة من ارتفاع 10 أمتار وقاسوا موقعها بمرور الوقت. مع كل ارتداد ، تفقد الكرة بعض ارتفاعها الأصلي:

لاحظ العلماء أن الكرة تفقد %20 من ارتفاعها بعد كل ارتداد. بعبارة أخرى ، يبلغ الحد الأقصى لارتفاع كل ارتداد %80 من الارتداد السابق. هذا سمح لهم بالتنبؤ بارتفاع كل ارتداد التالية:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

التعريفات

|إذا قارنت هاتين المشكلتين ، فقد تلاحظ أن هناك العديد من أوجه التشابه: تسلسل مذنب هالي له نفس بين الفترات المتتالية ، في حين أن تسلسل ارتداد الكرة له نفس نسبة بين الفصول المتتالية.

التسلسلات مع هذه الخصائص لها اسم خاص:

التسلسل الحسابي له فرق ثابت بين الفترات المتتالية.

يتم إضافة أو طرح نفس الرقم لكل مصطلح ، لإنتاج المصطلح التالي.

التسلسل الهندسي له نسبة ثابتة بين الفترات المتتالية.

يتم ضرب أو قسمة كل مصطلح على نفس العدد لإنتاج التالي.

فيما يلي بعض التسلسلات المختلفة. هل يمكنك تحديد القيم الحسابية أو الهندسية أو لا ، وما هي قيم d و r?

2 ، 4 ، 8 ، 16 ، 32 ، 64 ، ...

هي ، بنسبة .

2 ، 5 ، 8 ، 11 ، 14 ، 17 ، ...

هو ، مع فرق .

17 ، 13 ، 9 ، 5 ، 1 ، –3 ، ...

هو ، مع فرق .

2 ، 4 ، 7 ، 11 ، 16 ، 22 ، ...

هو .

40 ، 20 ، 10 ، 5 ، 2.5 ، 1.25 ، ...

هي ، بنسبة .

لتحديد تسلسل حسابي أو هندسي ، يجب أن نعرف ليس فقط الاختلاف أو النسبة المشتركة ، ولكن أيضًا القيمة الأولية (تسمى a). هنا يمكنك إنشاء تسلسلاتك الخاصة ورسم قيمها على رسم بياني ، بتغيير قيم a و د و ص. هل تستطيع ايجاد اي انماط؟

التسلسل الحسابي

a = ${a} ، d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

التسلسل الهندسي

a = ${b} ، r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

لاحظ كيف تبدو جميع التسلسلات الحسابية متشابهة جدًا: إذا كان الفرق إيجابيًا ، فإنها بثبات ، وإذا كان الفرق سلبيًا ، فإنه[بثبات|تزيد]].

من ناحية أخرى ، يمكن أن تتصرف التسلسلات الهندسية بشكل مختلف تمامًا استنادًا إلى قيم a و r:

إذا ، فإن الشروط حتى اللانهاية. يقول علماء الرياضيات أن التسلسل تتباعد

إذا كان ، فستقترب البنود . نقول أن التسلسل يتقارب.

إذا كانت ، فستتبادل المصطلحات بين الإيجابية والسلبية ، بينما تصبح أكبر.

سوف تتعلم المزيد حول التقارب والاختلاف في القسم الأخير من هذه الدورة.

صيغ تعاودية وصريحة

في القسم السابق ، علمت أن صيغة تعاودية تخبرك بقيمة كل مصطلح كدالة للمصطلحات السابقة. فيما يلي الصيغ العودية للتسلسلات الحسابية والهندسية:

xn=

تتمثل إحدى مشكلات الصيغ العودية في أنه للعثور على الحد 100 ، على سبيل المثال ، يتعين علينا أولاً حساب المصطلحات الـ 99 السابقة - وقد يستغرق ذلك وقتًا طويلاً. بدلاً من ذلك ، يمكننا محاولة العثور على صيغة صريحة ، تخبرنا بقيمة الحد n مباشرة.

بالنسبة إلى التسلسلات الحسابية ، يتعين علينا إضافة يوم في كل خطوة:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

في الفصل رقم ، نضيف نسخًا من يوم ، لذا فإن الصيغة العامة هي

xn=a+d×n−1

من أجل تسلسل هندسي ، علينا ضرب ص في كل خطوة:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

في الحد رقم ، نضرب نسخًا من ص ، لذا فإن الصيغة العامة

xn=a×rn−1

في ما يلي ملخص لجميع التعريفات والصيغ التي رأيتها حتى الآن:

تسلسل حسابي له المصطلح الأول a والفرق المشترك d بين المصطلحات المتتالية.

الصيغة العودية: xn=xn−1+d

صيغة صريحة: xn=a+d×n−1

تسلسل هندسي له الحد الأول a والنسبة الشائعة r بين الفترات المتتالية.

الصيغة العودية: xn=xn−1×r

صيغة صريحة: xn=a×rn−1

الآن دعونا نلقي نظرة على بعض الأمثلة حيث يمكننا استخدام كل هذا!

ادفعه للأمام

في ما يلي مقطع قصير من فيلم Pay it Forward ، حيث يشرح تريفور البالغ من العمر 12 عامًا فكرته عن جعل العالم مكانًا أفضل:

إن جوهر فكرة تريفور هو أنه إذا "دفعها الجميع إلى الأمام" ، يمكن لشخص واحد أن يكون له تأثير كبير على العالم:

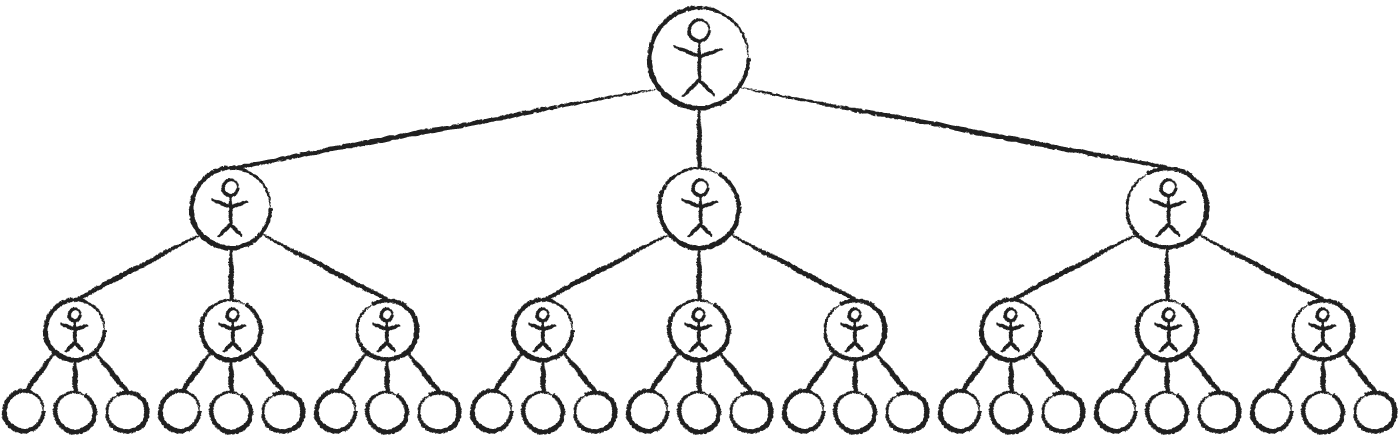
لاحظ كيف يشكل عدد الأشخاص في كل خطوة ، بنسبة مشتركة :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

باستخدام الصيغة الصريحة للتسلسلات الهندسية ، يمكننا معرفة عدد الأشخاص الجدد المتأثرين في أي خطوة:

xn =

يزداد عدد الأشخاص بسرعة لا تصدق. في الخطوة العاشرة ، ستصل إلى 19،683 جديدًا ، وبعد 22 خطوة ، كنت ستصل إلى عدد أكبر من الأشخاص الذين هم على قيد الحياة حاليًا على الأرض.

هذا التسلسل من الأرقام له اسم خاص: قوى 3. كما ترى ، كل مصطلح هو في الواقع مجرد قوة مختلفة من 3:

30, 31, 32, 33, 34, 35, …

من يريد أن يكون مليونيرا؟

قريبًا!

مشكلة رقعة الشطرنج

قريبًا!

تغيير اللغة

سجّل الدخول إلى Mathigon

شارك

إعادة تعيين التقدم

قائمة المصطلحات