مضلعات ومتعددة الوجوهالمواد الصلبة الأفلاطونية

في بداية هذه الدورة ، قمنا بتعريف المصلع العادي أنها "متماثلة" بشكل خاص ، حيث تكون جميع الجوانب والزوايا متشابهة. يمكننا القيام بشيء مماثل للعديد من الوجوه.

في متعدد الوجوه العادي ، تكون جميع الوجوه من نفس النوع من المضلع المنتظم ، ويقابل نفس العدد من الوجوه في كل رأس . تسمى متعدد الوجوه مع هاتين الخاصيتين بالجوامد الأفلاطونية الصلبة ، التي سميت باسم الفيلسوف اليوناني أفلاطون .

إذن كيف تبدو المواد الصلبة الأفلاطونية - وكم منها موجودة؟ لإنشاء شكل ثلاثي الأبعاد ، نحتاج إلى وجوه على الأقل لمقابلتها في كل قمة. لنبدأ بشكل منتظم بأصغر مضلع منتظم: مثلثات متساوية الأضلاع:

كما أن سبعة مثلثات أو أكثر في كل رأس لا تنتج أيضًا العديد من الأشكال المتعددة الوجوه: لا توجد مساحة كافية حول الرأس ، لتناسب العديد من المثلثات.

هذا يعني أننا وجدنا مواد صلبة أفلاطونية تتكون من مثلثات. دعنا ننتقل إلى المضلع المنتظم التالي: المربعات.

بعد ذلك ، دعنا نجرب الخماسي المنتظم:

إذا اجتمعت خماسي في كل رأس ، نحصل على Dodecahedron . لها . ("Dodeca" تعني "اثنا عشر" باليونانية.)

المضلع المنتظم التالي الذي يجب تجربته هو السداسيات:

إذا اجتمعت ثلاث سداسيات في كل قمة ، نحصل على الفور على التغطية بالفسيفساء متعدد الوجوه سداسي . نظرًا لعدم وجود مساحة لأكثر من ثلاثة ، يبدو أنه لا توجد مواد صلبة أفلاطونية تتكون من سداسيات.

يحدث نفس الشيء أيضًا لجميع المضلعات المنتظمة ذات أكثر من ستة جوانب. إنهم لا يغطون الشمع ، وبالتأكيد لا نحصل على أي مضلعات ثلاثية الأبعاد.

هذا يعني أن هناك مواد صلبة أفلاطونية فقط! دعنا نلقي نظرة عليها جميعًا معًا:

لاحظ كيف يتم عدد الوجوه والرؤوس حولها الشيء نفسه بالنسبة للمكعبات والثماني السطوح ، وكذلك الاثني عشر والسطوح المتساقطة ، بينما عدد الحواف كما هو مختلفة . تسمى هذه الأزواج من المواد الصلبة الأفلاطونية بمواد صلبة مزدوجة .

يمكننا تحويل متعدد الوجوه إلى ثنائيته ، عن طريق "استبدال" كل وجه برأس ، وكل رأس بوجه. تظهر هذه الرسوم المتحركة كيف:

إن رباعي الأسطح ثنائي مع نفسه. نظرًا لأنه يحتوي على نفس العدد من الوجوه والرؤوس ، فإن تبديلها لن يغير أي شيء.

يعتقد أفلاطون أن جميع المواد في الكون تتكون من أربعة عناصر: الهواء والأرض والماء والنار. كان يعتقد أن كل عنصر يتوافق مع واحدة من المواد الصلبة الأفلاطونية ، في حين أن العنصر الخامس سيمثل الكون ككل. نعلم اليوم أن هناك أكثر من 100 عنصر مختلف يتكون من ذرات كروية ، وليس متعدد الوجوه.

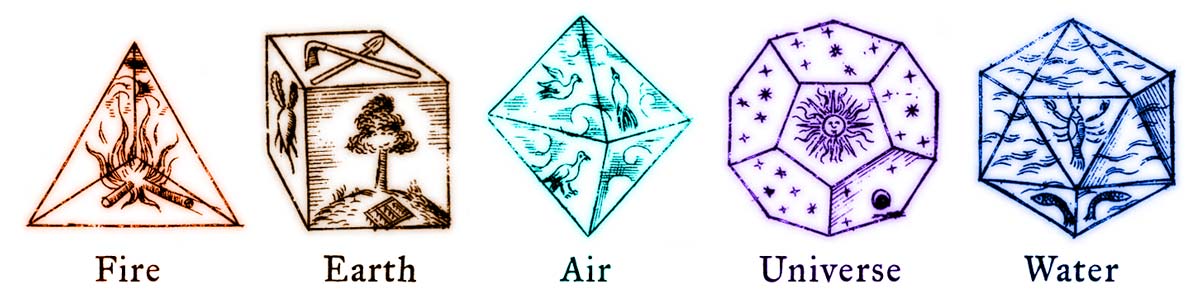
صور من كتاب يوهانس كيبلر “Harmonices Mundi” (1619)

المواد الصلبة الأرخميدية

المواد الصلبة الأفلاطونية هي متعددة الوجوه بشكل خاص ، ولكن هناك عدد لا يحصى من الآخرين.

على سبيل المثال ، يجب أن تتكون المواد الصلبة الأرخميدية من مضلعات عادية ، ولكن يمكنك استخدام أنواع مختلفة متعددة. تم تسميتهم على اسم عالم رياضيات يوناني آخر ، أرخميدس من سيراكيوز ، وهناك 13 منهم:

التطبيقات

كان أفلاطون مخطئًا في الاعتقاد بأن جميع العناصر تتكون من المواد الصلبة الأفلاطونية. لكن للعديد من الوجوه العادية العديد من الخصائص الخاصة التي تجعلها تظهر في مكان آخر في الطبيعة - ويمكننا نسخ هذه الخصائص في العلوم والهندسة.