مضلعات ومتعددة الوجوهالتغطية بالفسيفساء

تظهر المضلعات في كل مكان في الطبيعة. إنها مفيدة بشكل خاص إذا كنت تريد تجانب مساحة كبيرة ، لأنه يمكنك احتواء المضلعات معًا دون أي فجوات أو تداخلات. تسمى مثل هذه الأنماط التغطية بالفسيفساء .

نسخ البشر العديد من هذه الأنماط الطبيعية في الفن والهندسة المعمارية والتكنولوجيا - من روما القديمة حتى الوقت الحاضر. وفيما يلي بعض الأمثلة على ذلك:

هنا يمكنك إنشاء التغطية الفسيفساء الخاصة بك باستخدام المضلعات العادية. ما عليك سوى سحب الأشكال الجديدة من الشريط الجانبي إلى اللوحة القماشية. ما هي الأشكال الفسيفساء بشكل جيد؟ هل هناك أي أشكال لا تكسو على الإطلاق؟ حاول إنشاء أنماط مثيرة للاهتمام!

أمثلة على التغطية الفسيفساء الطلاب الآخرين

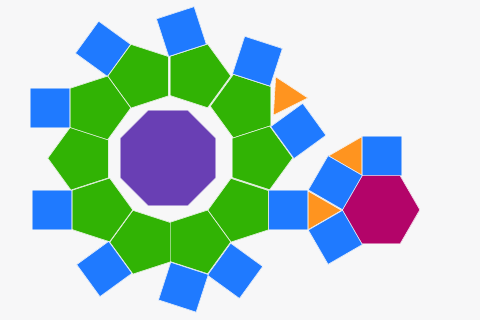
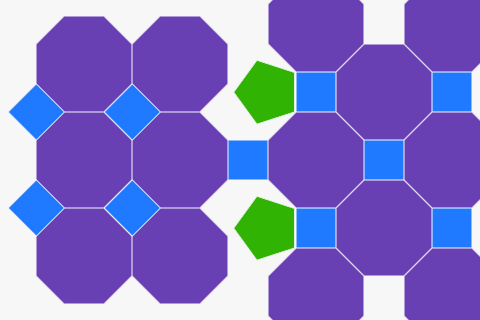
التغطية بالفسيفساء من المضلعات العادية

ربما لاحظت أن بعض المضلعات العادية (مثل المربعات الخماسي ) التغطية بالفسيفساء بسهولة جدا ، في حين أن الآخرين (مثل الخماسي مثلثات السداسيات ) لا يبدو التغطية بالفسيفساء على الإطلاق.

يتعلق هذا بحجم الزوايا الداخلية ، التي تعلمنا حسابها من قبل. عند كل رأس في التغطية بالفسيفساء ، تلتقي الزوايا الداخلية للعديد من المضلعات المختلفة. نحتاج إلى كل هذه الزوايا لإضافة ° ، وإلا سيكون هناك فجوة أو تداخل.

يمكنك أيضًا التحقق من ذلك ، تمامًا مثل الخماسي ، فإن أي مضلع عادي به 7 جوانب أو أكثر لا يتم تغطية الأرض. هذا يعني أن المضلعات العادية الوحيدة التي تغطي الفسيفساء هي مثلثات ومربعات وسداسيات!

بالطبع يمكنك الجمع بين أنواع مختلفة من المضلعات العادية في التغطية بالفسيفساء ، بشرط أن تضيف زواياها الداخلية ما يصل إلى 360 درجة:

مربعات والمثلثات
90° + 90° + 60° + 60° + 60° = 360°

مربعات والمثلثات
90° + 90° + 60° + 60° + 60° = 360°

السداسيات والمثلثات
120° + 120° + 60° + 60° = 360°

السداسيات والمثلثات
120° + 60° + 60° + 60° + 60° = 360°

السداسيات والمربعات والمثلثات
120° + 90° + 90° + 60° = 360°

المثمنات والمربعات
135° + 135° + 90° = 360°

Dodecagons (12-gons) والمثلثات
150° + 150° + 60° = 360°

Dodecagons, السداسيات والمربعات
150° + 120° + 90° = 360°

التغطية بالفسيفساء من مضلعات غير العادية

يمكننا أيضًا تجربة صنع الفسيفساء من المضلعات غير العادية - طالما أننا حريصون عند تدويرها وترتيبها.

البنتاغون أصعب قليلاً. لقد رأينا بالفعل أن الخماسي المنتظم لا التغطية بالفسيفس التغطية بالفسيفساء ، ولكن ماذا عن تلك غير العادية؟

فيما يلي ثلاثة أمثلة مختلفة للفسيفساء مع الخماسي. إنها ليست منتظمة ، لكنها مضلعات صالحة تمامًا من 5 جوانب.

حتى الآن ، وجد علماء الرياضيات 15 نوعًا مختلفًا من الفسيفساء مع خماسي (محدب) - تم اكتشاف أحدثها في عام 2015. لا أحد يعرف ما إذا كان هناك أي أنواع أخرى ، أو إذا كان هؤلاء الخمسة عشر هم الوحيدون ...

التغطية بالفسيفساء في الفن

كانت التغطية بالفسيفساء أداة وإلهام للعديد من الفنانين والمهندسين المعماريين والمصمم - أشهرها الفنان الهولندي موريتس كورنيليس إيشر . يحتوي عمل ايشر على مخلوقات وأنماط ومناظر طبيعية غريبة ومتغيرة:

غالبًا ما تبدو هذه الأعمال الفنية ممتعة وبلا مجهود ، ولكن المبادئ الرياضية الأساسية هي نفسها كما كانت من قبل: الزوايا والتناوب والترجمات والمضلعات. إذا لم تكن الرياضيات صحيحة ، فإن التغطية بالفسيفساء لن تعمل!

“التحول II by M. C. Escher (1940)

تبليط بنروز

جميع الفسيفساء التي رأيناها حتى الآن تشترك في شيء واحد: أنها دورية . هذا يعني أنها تتكون من نمط منتظم يتكرر مرارًا وتكرارًا. يمكن أن تستمر إلى الأبد في جميع الاتجاهات وسوف تبدو متشابهة في كل مكان.

في السبعينيات ، اكتشف عالم الرياضيات والفيزيائي البريطاني روجر بنروز الفسيفساء غير الدورية - لا تزال مستمرة إلى ما لا نهاية في جميع الاتجاهات ، لكنها لا تبدو متشابهة تمامًا. تسمى هذه المربعات بنروز ، وتحتاج فقط إلى أنواع مختلفة من المضلعات لإنشاء واحد:

كان بنروز يستكشف التغطية بالفسيفساء لمجرد التسلية ، ولكن اتضح أن البنية الداخلية لبعض المواد الحقيقية (مثل الألومنيوم) تتبع نمطًا مشابهًا. تم استخدام النمط حتى على ورق التواليت ، لأن الشركات المصنعة لاحظت أنه يمكن لف النمط غير الدوري دون أي انتفاخات.