التحولات والتماثلمجموعات التماثل والخلفيات








لقد سبق ووضحت أعلاه أن المربع به
كما أن لديها تماثل دوراني بمقدار
وأخيرًا ، يمكننا التفكير في "عدم فعل أي شيء" كنوع خاص آخر من تماثل - لأن النتيجة (من الواضح) هي نفسها كما كانت من قبل. يُسمى هذا أحيانًا الهوية.
في المجموع ، وجدنا
الآن يمكننا بالفعل البدء في إجراء بعض العمليات الحسابية باستخدام هذه التماثلات. على سبيل المثال ، يمكننا إضافة تماثلين للحصول على تماثل جديد:






عندما تضيف تماثلين من مربع ، الحصول على واحدة جديدة. إليك "الآلة الحاسبة للتماثل" حيث يمكنك تجربتها بنفسك:
اقض بعض الوقت في اللعب باستخدام الآلة الحاسبة للتماثل ، وحاول العثور على أي أنماط. هل يمكنك إكمال هذه الملاحظات؟ * تؤدي إضافة دورتين إلى منح
ربما أدركت بالفعل أن إضافة تحولات تشبه إلى حد كبير إضافة أعداد صحيحة:
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
في الرياضيات ، أي مجموعة لها هذه الخصائص تسمى
على سبيل المثال ، يمكن لمجموعات التماثل للجزيئات المختلفة مساعدة العلماء على التنبؤ بخصائص المواد المقابلة وتفسيرها. يمكن أيضًا استخدام المجموعات لتحليل الإستراتيجية الفائزة في ألعاب الطاولة وسلوك الفيروسات في الطب والتوافقيات المختلفة في الموسيقى والعديد من المفاهيم الأخرى ...
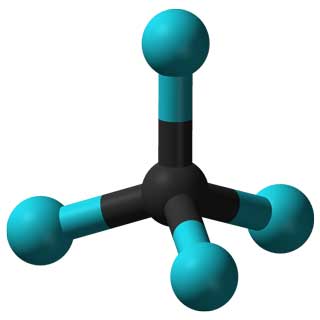
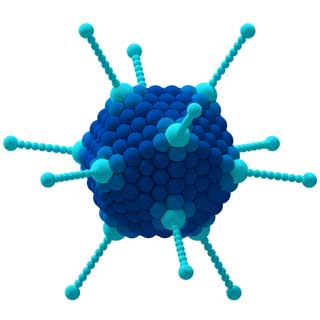
خصائص جزيء CCl 4 (يسار) والفيروسات الغدية (اليمنى) يحددها تناظرهما.
مجموعات ورق الحائط
في الأقسام السابقة شاهدنا نوعين مختلفين من تلتماثل يتوافقان مع تحولين مختلفين: التدوير والانعكاسات. ولكن هناك أيضًا تناظر للنوع الثالث من التحول الجامد:


قرد هوني سداسي


بلاط سيراميك للحوائط
بالإضافة إلى التناظر الانعكاسي والتناوب والانتقالي ، هناك نوع رابع:


يمكن أن يحتوي النمط على أكثر من نوع واحد من التناظر. ومثلما هو الحال بالنسبة للمربعات ، يمكننا العثور على
تخبرك هذه المجموعات كثيرًا عن كيفية ظهور النمط لا (مثل ألوانه وأشكاله) ، فقط كيف يتكرر. يمكن أن يكون للعديد من الأنماط المختلفة نفس مجموعة التماثل - طالما يتم ترتيبها وتكرارها بنفس الطريقة.


لهذين النمطين نفس التماثلات ، على الرغم من أنهما مختلفان تمامًا. لكن التماثلات لا تتعلق بالألوان أو الأشكال السطحية.


يتمتع هذان النمطان أيضًا بنفس التماثلات - على الرغم من أنهما يبدوان أكثر تشابهًا مع الأنماط المقابلة على اليسار ، مقارنة ببعضهما البعض.
اتضح أنه ، في حين أن هناك العديد من الأنماط الممكنة بشكل لا نهائي ، إلا أنها تحتوي جميعها على واحدة من 17 مجموعة تماثل مختلفة. تسمى هذه مجموعات ورق الحائط. يتم تعريف كل مجموعة ورق حائط من خلال مجموعة من الترجمات والتناوب والانعكاسات وانعكاسات الانزلاق. هل يمكنك مشاهدة

Type P1
إنتقالات فقط

Type P2
Rotations of order 2, translations

Type P3
Rotations of order 3 (120°), translations

Type P4
Four rotations of order 2 (180°), translations

Type P6
Rotations of order 2, 3 and 6 (60°), translations

Type PM
Parallel axes of reflection, translations

Type PMM
Perpendicular reflections, rotations of order 2, translations

Type P4M
Rotations (ord 2 + 4), reflections, glide reflections, translations

Type P6M
Rotations (ord 2 + 6), reflections, glide reflections, translations

Type P3M1
Rotations of order 3, reflections, glide reflections, translations

Type P31M
Rotations of order 3, reflections, glide reflections, translations

Type P4G
Rotations (ord 2 + 4), reflections, glide reflections, translations

Type CMM
Perpendicular reflections, rotations of order 2, translations

Type PMG
Reflections, glide reflections, rotations of order 2, translations

Type PG
Parallel glide reflections, translations

Type CM
Reflections, glide reflections, translations

Type PGG
Perpendicular glide reflections, rotations of order 2, translations
للأسف ليس هناك سبب بسيط لوجود 17 من هذه المجموعات. إثبات ذلك يتطلب رياضيات أكثر تقدمًا ...
بدلاً من ذلك ، يمكنك محاولة رسم الأنماط المتكررة الخاصة بك لكل مجموعة من خلفيات الشاشة الـ 17:
مثال على رسومات الطلاب الآخرين



كانت مجموعات ورق الحائط تدور حول أنماط مسطحة وثنائية الأبعاد. يمكننا أن نفعل شيئًا مشابهًا للأنماط ثلاثية الأبعاد: تسمى هذه المجموعات البلورية ، وهناك 219 منهم!
بالإضافة إلى الترجمات والانعكاسات والتدوير وانعكاسات الانزلاق ، تتضمن هذه المجموعات تناظرًا مثل مستويات انزلاق و محاور لولبية (فكر في الحركة عند فك الزجاجة).
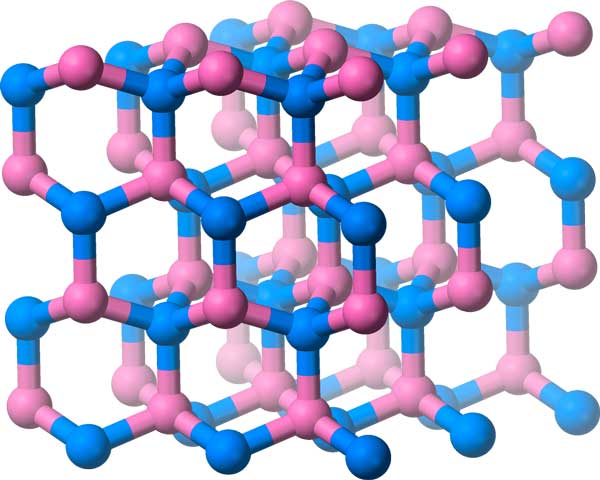
يحتوي Boron-Nitride على جزيئاته مرتبة في هذه الشبكة البلورية ، التي تحتوي على مجموعة تناظر ثلاثية الأبعاد.