فركتلاتمقدمة

عند النظر حول الطبيعة ، ربما لاحظت نباتات معقدة مثل هذه:

يتكون هذا السرخس من العديد من الأوراق الصغيرة التي تتفرع من أكبر.

يتكون Romanesco broccoli من أصغر تدور حول واحدة أكبر.

في البداية ، تبدو هذه الأشكال معقدة للغاية - ولكن عندما تنظر عن قرب ، قد تلاحظ أن كلاهما يتبع نمطًا بسيطًا نسبيًا: تبدو جميع الأجزاء الفردية للنباتات تمامًا مثل كامل النبات ، أصغر فقط. يتم تكرار نفس النمط مرارًا وتكرارًا بمقاييس أصغر.

في الرياضيات ، نسمي هذه الخاصية تشابه ذاتي ، والأشكال التي تسمى فركتلات. هم بعض من أجمل وأجمل الأشياء في كل الرياضيات.

لإنشاء الفركتلات الخاصة بنا ، يجب أن نبدأ بنمط بسيط ثم نكرره مرارًا وتكرارًا بمقاييس أصغر.

قد يكون أحد أبسط الأنماط هو مقطع سطر ، مع مقطعين آخرين يتفرعان من طرف واحد. إذا كررنا هذا النمط ، فسيكون لكل من هذه الأجزاء الزرقاء فرعين آخرين في نهايتيهما.

يمكنك تحريك النقاط الزرقاء لتغيير طول جميع الفروع وزاويتها. ثم قم بزيادة عدد التكرارات باستخدام شريط التمرير أدناه.

بناءً على موضع الفروع ، يمكنك عمل أنماط مختلفة تمامًا - تبدو مثل أعلاه ، أو ، أو . ماذا يمكنك أن تجد؟

فركتات اخقرة هومثلث سيربينسكس . في هذه الحالة ، نبدأ بمثلث كبير متساوي الأضلاع ، ثم نقطع بشكل متكرر المثلثات الأصغر من الأجزاء المتبقية.

لاحظ كيف يتكون الشكل النهائي من ثلاث نسخ متطابقة منه ، وكل منها تتكون من نسخ أصغر من المثلث بأكمله! يمكنك الاستمرار في تكبير المثلث إلى الأبد ، وستستمر الأنماط والأشكال في التكرار دائمًا.

تبدو النباتات في بداية هذا الفصل حقيقية في الحياة الواقعية. إذا واصلنا تكرار نفس النمط مرارًا وتكرارًا ، أصغر وأصغر ، فسنصل في النهاية إلى الخلايا أو الجزيئات أو الذرات التي لم يعد من الممكن تقسيمها.

ومع ذلك ، باستخدام الرياضيات ، يمكننا التفكير في الخصائص التي قد يمتلكها الفركتلات الحقيقية - وهذه مفاجأة جدًا…

أبعاد الفراكتل

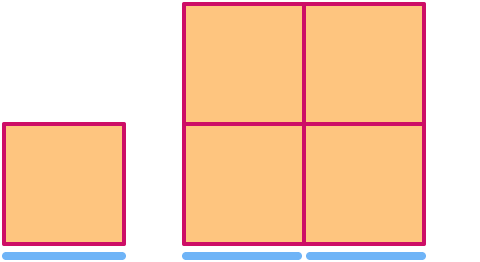
أولاً ، دعونا نفكر في أبعاد الفركتلات. للخط بُعد . عند قياسه بعامل 2 ، يزيد طوله بعامل 21=2. من الواضح!

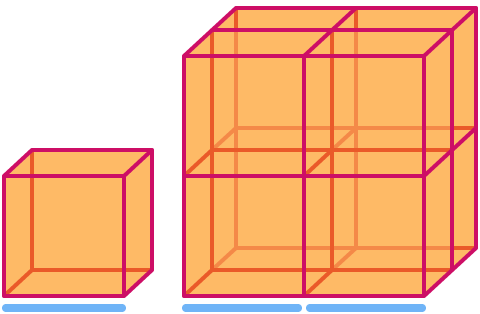
المربع له أبعاد . عند قياسه بعامل 2 ، تزداد مساحته بعامل 22= .

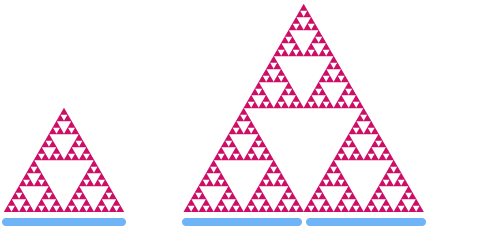
المكعب له أبعاد . عند قياسه بعامل 2 ، يزداد حجمه بعامل 23= . لاحظ أن المكعب الأكبر في الصورة يتكون من 8 نسخ من النسخة الأصغر!

الآن دعونا نلقي نظرة على مثلث سيربينسكي. إذا قمنا بقياسها بعامل 2 ، يمكنك أن ترى أن "المساحة" تزداد بعامل .

فلنفترض أن d هو بُعد مثلث سيربينسكي. باستخدام نفس النمط أعلاه ، نحصل على 2d=3. بمعنى آخر ، يوم = ≈ 1.585…

ولكن انتظر ... كيف يمكن أن يكون لشيء بعد ليس عددًا صحيحًا؟ يبدو الأمر مستحيلًا ، لكن هذه ليست سوى واحدة من الخصائص الغريبة للفركتلات. في الواقع ، هذا هو ما يعطي الكسور اسمها: لديهم بعد كسري.

مع كل تكرار ، نزيل بعض مساحة مثلث سيربينسكي. إذا تمكنا من فعل ذلك بشكل لا نهائي عدة مرات ، فلن تكون هناك مساحة متبقية في الواقع: لهذا السبب فإن مثلث سيربينسكي هو شيء بين منطقة ثنائية الأبعاد وخط أحادي البعد.

في حين أن العديد من الفركتلات متشابهة ذاتيًا ، فإن التعريف الأفضل هو أن الفركتلات هي أشكال لها بُعد غير صحيح.

كوخ ندفة الثلج

هناك العديد من الأشكال في الطبيعة التي تبدو مثل الفركتلات. لقد رأينا بالفعل بعض النباتات في بداية هذا الفصل. من الأمثلة الرائعة الأخرى رقاقات الثلج وبلورات الثلج:

لإنشاء ندفة ثلجية كسورية خاصة بنا ، يتعين علينا مرة أخرى إيجاد إجراء بسيط يمكننا تطبيقه مرارًا وتكرارًا.

مثل مثلث سيربينسكي ، لنبدأ بمثلث واحد متساوي الأضلاع. ومع ذلك ، بدلاً من إزالة مثلثات أصغر في كل خطوة ، نضيف مثلثات أصغر على طول الحافة. الطول الجانبي لكل مثلث هو من المثلثات في الخطوة السابقة.

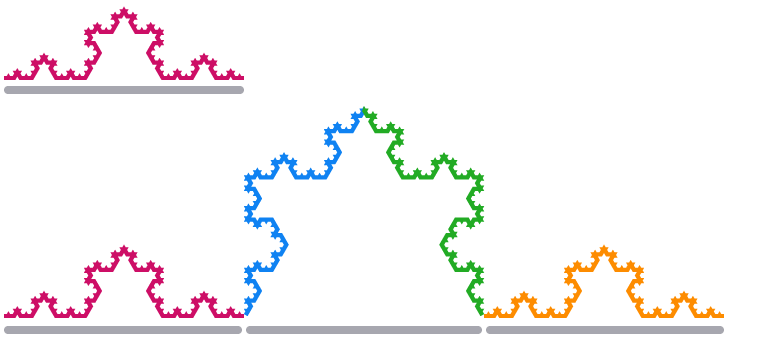
يسمى الشكل الناتجــكخفةلثلخ ، والتي تحمل اسم عالم الرياضيات السويدي هيلج فون كوخ. لاحظ مرة أخرى أن أجزاء صغيرة من حافة ندفة الثلج تبدو تمامًا مثل أقسام أكبر.

عندما نقوم بقياس جزء حافة واحدة من كوخ ندفة الثلج بمعامل 3 ، يبلغ طوله .

باستخدام نفس العلاقة بين الأبعاد وعوامل القياس الموضحة أعلاه ، نحصل على المعادلة . وهذا يعني أن بُعد كوخ ندفة الثلج هو d=log34≈1.262.

المساحة

يشبه إنشاء رقائق كوخ الثلجية تسلسلًا تعاوديًا: فنحن نعرف شكل البداية (مثلث) ونعرف كيفية الانتقال من مصطلح إلى آخر (بإضافة المزيد من المثلثات على كل حافة):

مثلثات جديدة

بعد التكرار الأول ، يزداد عدد المثلثات الجديدة المضافة بمقدار في كل خطوة. في الوقت نفسه ، تقل مساحة هذه المثلثات الجديدة بمعامل في كل خطوة.

لنفترض أن المثلث الأول تبلغ مساحته 1. ثم تبلغ المساحة الإجمالية لـ المثلثات الثلاثة التالية هي 3×19=13. تشكل جميع الخطوات التالية ، بنسبة مشتركة .

باستخدام صيغة مجموع سلسلة هندسية غير محدودة ، يمكننا حساب أن المساحة الإجمالية لثلج ندفة الثلج هي

A=1+13×1=85=1.6.

المحيط

يمكننا أيضًا محاولة حساب محيط ندفة الثلج كوخ. كما رأينا من قبل ، يتغير طول المحيط بعامل في كل خطوة.

هذا يعني أنه لدينا مرة أخرى سلسلة هندسية - ولكن في هذه الحالة . وهذا يعني أن محيط ندفة الثلج كوخ هو في الواقع طويل بلا حدود!

إذا كان هذا يبدو غير بديهي ، فتذكر أننا نضرب المحيط في 43 في كل خطوة ، ونقوم بذلك بشكل لا نهائي عدة مرات.

لا يمكن التفكير تقريبًا في أنه يمكنك الحصول على شكل بمساحة محدودة وأيضًا محيط غير محدود - ولكن هذه ليست سوى واحدة من العديد من الخصائص غير المتوقعة للفركتلات.

هل يمكنك التوصل إلى أي طرق أخرى لإنشاء فركتلات خاصة بك؟

"روحي تتصاعد على فركتلات مجمدة في كل مكان ..."

إسفنجة مينجر

لا يجب أن تكون صور الكسيريات "مسطحة" ، مثل العديد من الأمثلة أعلاه. إحدى أشهر الفركتلات التي تبدو ثلاثية الأبعاد هي إسفنجة مينجر ، التي سميت باسم عالم الرياضيات كارل مينجر الذي وصفها لأول مرة في عام 1926.

نبدأ بمكعب صلب ، ونقوم بشكل متكرر بحفر ثقوب أصغر وأصغر في جوانبها. كل تكرار جديد للثقوب له عرض التكرار السابق للثقوب.

يتكون المكعب 3×3×3 من 27 مكعبًا أصغر حجمًا ، ولكن هنا أزلنا بعضًا منها. تتكون إسفنجة مينج من نسخة من نفسها ، وهي أصغر 3 مرات.

الآن يمكننا محاولة حساب البُعد d من الإسفنج مينحر تمامًا كما فعلنا مع كوج خ ندفة الثلج أعلاه. في هذه الحالة نحصل على 3d=20 أو d=log320≈2.727.

إذا كنت تتخيل قطع المزيد والمزيد من الثقوب ، بشكل لا نهائي عدة مرات ، فلن يتبقى حجم فعلي. هذا هو السبب في أن المكعب ثلاثي الأبعاد "ليس تمامًا"!

الخطوط الساحلية الفراكتالية

واحدة من الخصائص الرئيسية لجميع الفركتلات التي رأيناها حتى الآن هي أنه يمكنك "التكبير" إلى الأبد والعثور دائمًا على أنماط جديدة. في حوالي عام 1920 ، أدرك عالم الرياضيات البريطاني لويس فراي ريتشاردسون أن الشيء نفسه ينطبق على الحدود أو الخط الساحلي للعديد من البلدان.

تبدأ بالشكل الأساسي للبلد ، وعند التكبير ، تقوم بإضافة مداخل الأنهار والخلجان ومصبات الأنهار ، ثم المنحدرات والصخور والحصى الفردية وما إلى ذلك:

هذه مشكلة كبيرة عند محاولة حساب طول حدود بلد ما - كيف تقرر مدى التكبير ، وأي الزوايا والشقوق التي يجب تضمينها؟

إحدى الطرق التي يمكننا من خلالها قياس طول السواحل البريطانية ، على سبيل المثال ، هي أخذ مسطرة طويلة ، والمشي على طول الطريق حول شواطئها ، ثم جمع كل المسافات.

إذا كان طول المسطرة ${rulers[index]} كم ، فيجب أن نستخدمها ${count} مرة ، لذا نحصل على خط ساحلي إجمالي ${count} × ${rulers[index]} = ${count * rulers[index]} كم.

يمكننا فقط الاستمرار مع الحكام الأصغر والأصغر ، وفي كل مرة ستصبح نتيجتنا على طول الخط الساحلي أطول قليلاً. تمامًا مثل كوخ ندفة الثلج من قبل ، يبدو أن الساحل البريطاني طويل جدًا! غالبًا ما يطلق عليه مفارقة الخط الساحلي.

بعد عقود قليلة ، تعثر عالم الرياضيات بنوا ماندميروت في عمل ريتشاردسون في كتاب مكتبة مهمل ، أثناء عمله في IBM. لقد أدرك أهميته ، وكذلك كيفية ارتباطه بأبحاث أحدث حول الفركتلات والأبعاد.

من المؤكد أن الخط الساحلي لبريطانيا "يبدو" كسورية ، لكنه ليس مشابهًا لنفسه ، مثل صور النمطي هندسي متكرر أخرى رأيناها من قبل. من أجل العثور على حجمه ، يمكننا رسمه على شبكة وحساب عدد الخلايا التي يتقاطع معها.

في البداية ، هناك 88 خلايا متقاطعة. إذا قمنا بقياس الخط الساحلي بمعامل 2 ، فهناك 197 من الخلايا المتقاطعة - أكثر من ضعف العدد!

زاد حجم الخط الساحلي بمعامل 19788. كما كان من قبل ، هذا يعني أن أبعاد الخط الساحلي

d=log219788≈1.16

إذا كررنا ذلك بشبكات أكبر ، فسنجد أن بُعد الخط الساحلي لبريطانيا يبلغ تقريبًا 1.21. أدرك ماندلبروت أن هذا البعد الكسري هو أيضًا مقياس خشونة الشكل - مفهوم جديد ، وجد له تطبيقات مهمة في العديد من المجالات الأخرى للرياضيات والعلوم.

قائمة المصطلحات

فركتلاتمقدمة

أبعاد الفراكتل

كوخ ندفة الثلج

المساحة

المحيط

إسفنجة مينجر

الخطوط الساحلية الفراكتالية

المزيد مر الفركتلات في الطبيعة و التكنولوجيا

تغيير اللغة

سجّل الدخول إلى Mathigon

شارك

إعادة تعيين التقدم

قائمة المصطلحات

فركتلاتمقدمة

أبعاد الفراكتل

كوخ ندفة الثلج

المساحة

المحيط

إسفنجة مينجر

الخطوط الساحلية الفراكتالية

المزيد مر الفركتلات في الطبيعة و التكنولوجيا